看到昨天，應該對機器學習不再畏懼了吧！也大概對機器學習有所認識了，接下來要分享的是機器學習中非常基礎的概念－線性回歸分析(linear regression)。

線性回歸(linear regression)

介紹

依照餵給機器的訓練資料找出一個最接近各點線性方程式(就是昨天提到的最好的函式F)，並用這個函式F去預測出新的資料(測試資料)應該在的位置。線性回歸也是監督學習的一種。

在統計學中，也有出現過這個名詞，其實是類似的概念，目的是用來在一個或是多個自變數(independent variable)和應變數(dependent variable)之間找出關係。
啥是自變數、啥是應變數？：自變數就是會自己改變的數，而應變數是會跟著自變數變而變的數，也就是今天自變數不變了，那應變數也不會改變。例如 y=ax+b，x就是自變數，當x改變了，y才跟著變化。

應用例子

1. 自駕車：車上的各種感應器會將感應到的數據收集起來，讓車子去判斷這個時間點是否要轉彎、轉幾度。
2. 推薦系統：廣告商會蒐集使用者的資訊(可能是你點擊某樣商品的次數、你的年紀資訊等等)，進而去判定出要推播什麼廣告給使用者，使用者的購買意願會最大，增加使用者的購買意願。
3. 房價預測：收集各項房子的資訊(如坪數、臥室數量、有無停車格等等)和當時賣出的價格，藉此找到最適當的函式，而可以判定出新的房子應該可以賣多少。

簡單的線性回歸例子

下圖JOHN國的房價，JOHN國的房價很簡單，只受到坪數大小的影響。
id | price | sqft_living
------------- | ----------
1 | 500000 | 55
2 | 275000 | 27
3 | 360000 | 33
4 | 780000 | 70
5 | 145000 | 13
6 | 280000 | 26
7 | 860000 | 89
8 | 200000 | 21
9 | 90000 | 10
10 | 680000 | 67

我們將他畫在圖上，縱軸是房價，橫軸是坪數大小：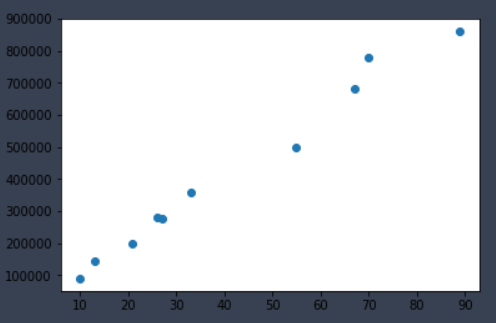

利用線性回歸的方法求出我們的函式F：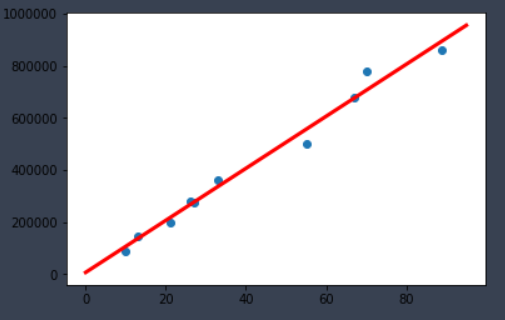

這條紅線就是JOHN國的房價預測模型，可以看出這個模型很逼近每間房子，我們也可以找出這個函式是：y(price)= 10088.793*x(sqft_living) + 180.113
因此當又有一棟新的房子蓋完，我們可以依照他的坪數去判定它在JOHN國應該可以賣的價錢！

今天只是提到線性回歸的介紹以及最簡單的線性回歸例子，上頭的圖都是用python撰寫的，等到基礎的數學理論、跟觀念分享完後，會開始分享程式如何撰寫，讓大家有將理論實際應用的感覺！

明天會開始提及有關Regression的重要方程式，而後天會開始介紹這些方程式，也是最吃數學的地方，等熬過這段，就可以進入到實際操演拉！加油加油！